Hauptsatz der Differential- und Integralrechnung
Die Berechnung der Fläche mit Hilfe von Unter- und Obersumme ist unbefriedigend, da es nur eine Näherung ist. Wir brauchen einen Zusammenhang zwischen f(x) und F(a,x), der es uns erlaubt, die Fläche exakt zu berechnen.
Hier hilft uns folgende Behauptung:
Hauptsatz der Differential- und Integralrechnung:
F'(a,x)
= f(x)
Das bedeutet: Wenn wir f(x) kennen, müssen wir nur eine Funktion F(x) finden,
deren Ableitung f(x) ergibt. So etwas nennt man eine Stammfunktion von
f(x).
Hinweis: Das konstante a spielt hier keine Rolle mehr, da konstante Summanden bei der Ableitung wegfallen. Die Stammfunktion ist daher nicht eindeutig. Beispiel: F(a,x) = x² + 3 ist ebenso eine Stammfunktion von f(x)=2x, wie F(a,x) = x² + 8 oder F(a,x) = x² + c. Das c hängt dann halt vom a ab (je weiter links das a, umso größer das c)
Beweis des Satzes:
Vereinfachung:
da a ohnehin konstant ist verwenden wir F(x) statt F(a,x). F(x) soll a in Form
einer Konstante schon beinhalten.
Erinnerung an den Differentialquotienten:
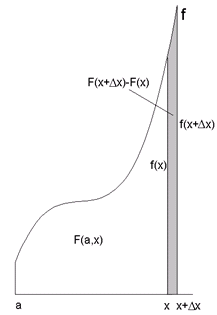
Der graue Streifen ist F(x+Δx)-F(x)
Es gilt:
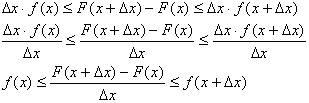
also: F'(x) = f(x) also ist F(x) eine Stammfunktion von f(x) (q.e.d).
Nutzen: Das bestimmte Integral 
(=die orientierte Fläche in den Grenzen a und b) kann also berechnet werden,
indem eine beliebige Stammfunktion F(x) von f(x) gesucht und auf die Grenzen
a und b angewendet wird. F(a,b) = F(b)-F(a).
Beispiel:
Übung
a) Zeige dass F(x) eine Flächenfunktion für die Funktion 
ist.
b) Berechne mit Hilfe von F die Fläche zwischen f(x) und der x-Achse im
Intervall [0; 4]
