Integralrechnung - Unter- und Obersumme
Nun gehen wir daran, die Fläche möglichst genau zu berechnen und zwar mithilfe einer Folge von Rechtecken. Das funktioniert auch dann, wenn wir keine Stammfungktion finden können.
Der Trick:
Wir berechnen den Flächeninhalt näherungsweise, indem wir die Fläche in rechteckige Streifen unterteilen, die ein bisschen kleiner als die Fläche sind und an einer Ecke die Kurve grad berühren (Untersumme). Dann machen wir die Rechnung noch einmal, aber diesmal mit Streifen, die ein wenig höher sind (Obersumme). Die wirkliche Fläche liegt dann zwischen Untersumme und Obersumme.
Verändere im Applet die Anzahl der Streifen (Schieberegler) um zu sehen, wie genau die Rechnung wird.
Reinhard Sepp, 27 August 2014, erstellt mit GeoGebra
Berechnung von Unter- und Obersumme
Aufgabe:
Berechne den Flächeninhalt zwischen Funktionsgraf und x-Achse im Intervall [0;4] näherungsweise als Summe von Rechtecken
Vorgangsweise:
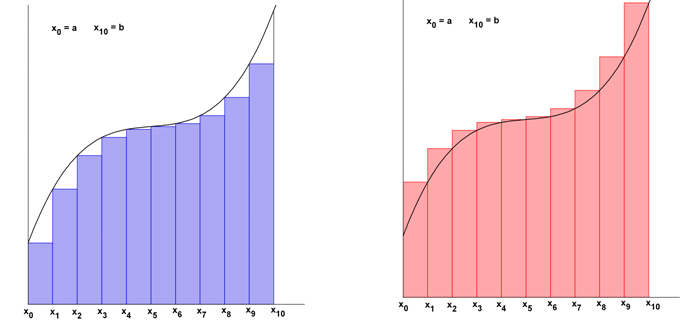
Bei der Untersumme werden die Eckpunkte x0, x1, x2, … xn-1 zur Berechnung
der Höhen f(xk) verwendet, also k = 0, 1, 2, … n-1.
Bei der Obersumme werden die Eckpunkte x1, x2, x3, … xn zur Berechnung der Höhen
f(xk) verwendet, also k = 1, 2, 3, … n.
Für
k = 0 erhält man a, für k = n erhält man b
Berechnung:
Übung
Berechne in Excel, Mathcad oder mit einem guten Taschenrechner mit Listenfunktionen die Untersumme und die Obersumme für n=10, 100, 1000, 10000
Hinweis: Das Dokument ober_untersummen_ti83.pdf erklärt auf Seite 2, wie man mit dem TI83 die Unter- und Obersumme berechnet (gefunden bei http://www.k-achilles.de/analysis/ober_untersummen_ti83.pdf)